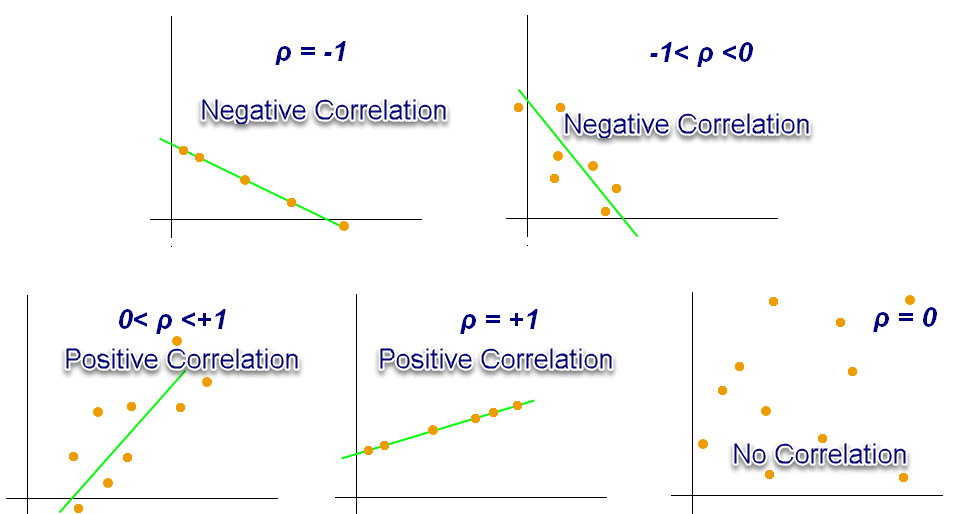
Correlation Coefficient Chart
This table shows the Pearson correlation critical values for different significance levels and degrees of freedom. Learn how to measure and interpret the strength and direction of the linear relationship between two continuous variables using Pearson's correlation coefficient. See graphs, examples, and formulas for different types of correlation coefficients.
Find critical values for two-tail tests of Pearson's correlation coefficient in this table. Download the Excel workbook with the table and see how to use it for hypothesis testing. Make Correlation Graph in Excel is done by following steps like creating dataset, naming the coordinate and formatting the graph.
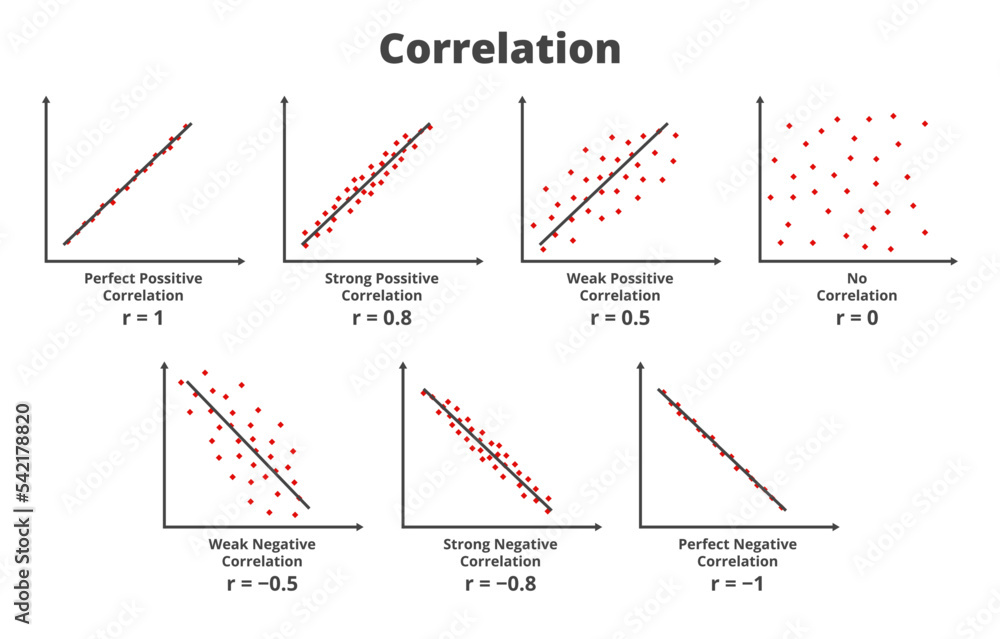
How to Calculate the Coefficient of Correlation
Pearson Correlation Coefficient Critical Values Table The values in the table are for a two tailed test with d.f. = n - 2. Reject H0: ρ = 0 if the absolute value of r is greater than the value given in the table.
/TC_3126228-how-to-calculate-the-correlation-coefficient-5aabeb313de423003610ee40.png "How to Calculate the Coefficient of Correlation")
Correlation basically means a mutual connection between two or more sets of data. In statistics, bivariate data or two random variables are used to find the correlation between them. Correlation coefficient is generally the measurement of correlation between the bivariate data which basically denotes how much two random variables are correlated with each other.
Correlation Analysis - Technique of Data Analysis
If the correlation coefficient. Need help conducting your Pearson Correlation? Leverage our 30+ years of experience and low-cost same-day service to complete your results today! Schedule now using the calendar below. Learn how to calculate and interpret correlation coefficient, build a correlation matrix and plot a correlation graph in Excel.
The tutorial covers Pearson correlation, formulas, data analysis and potential issues with correlation. Learn how to calculate and interpret correlation coefficients, which measure the strength and direction of a relationship between variables. See examples of different types of correlation coefficients and how to visualize them with charts.
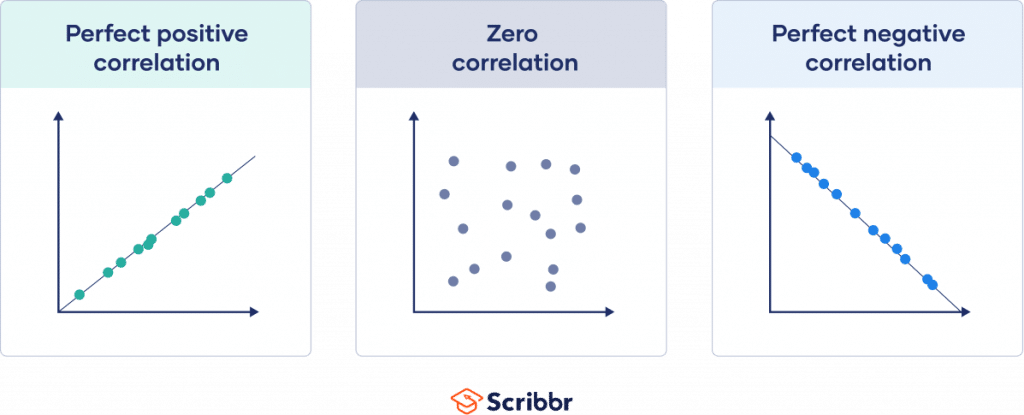
Correlation Coefficient Graph.svg
Critical Values of the Pearson Product-Moment Correlation Coefficient How to use this table df = n -2 Level of Significance (p) for Two.
