Coloring Tree Hackerrank
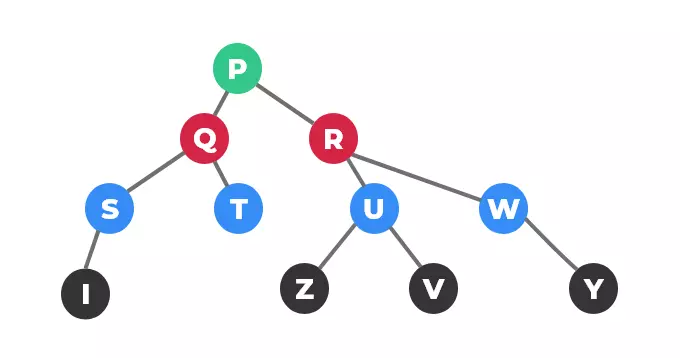
Given a tree with all nodes colored, find the number of distinct colors rooted at a given node. HackerRank Coloring Tree problem solutionIn this HackerRank Coloring Tree problem solution, you are given a tree with N nodes with every node being colored. A color is represented by an integer ranging from 1 to 109.

Can you find the number of distinct colors available in a subtree rooted at the node s? Copy The Code & Try With Live Editor Advertisements Demonstration Previous [Solved] Roy and alpha-beta trees solution in Hackerrank - Hacerrank solution C, C++, java,js, Python [Solved] Recalling Early Days GP with Trees solution in Hackerrank - Hacerrank solution C, C++, java,js, Python. My solutions to the challenges on HackerRank. Contribute to Gayathrichennaioutlook/HackerRank2 development by creating an account on GitHub.
HackerRank Black and White Tree Solution - TheCScience
HackerRank's programming challenges which are solved in programming languages (C, C++, Java, C#, Ruby, Linux Shell, AI, SQL, Regex, Python). You are given a tree with n nodes. You are required to color the tree with r colors.

Cost of coloring a node with color i is A i. Also, for each edge, such that the nodes at its end point are colored with the same color i, there is an additional cost of B i. You are required to find the minimum cost to color all the nodes of the tree.

[Hackerrank Solution] Mastering Binary Search Trees: Preorder, Inorder ...
Input The first line of the input contains 2 integers n. Given a tree with all nodes colored, find the number of distinct colors rooted at a given node. Solving code challenges on HackerRank is one of the best ways to prepare for programming interviews.
![[Hackerrank Solution] Mastering Binary Search Trees: Preorder, Inorder ... [Hackerrank Solution] Mastering Binary Search Trees: Preorder, Inorder ...](https://miro.medium.com/v2/resize:fit:1200/1*NqX5_RUz4eqHSrfzmpq3-Q.png)
HackerRank solutions. Contribute to aks47u/HackerRank development by creating an account on GitHub. Today when he got a tree, he colored each edge with one of either red (r) or black (b) color.

Nature, coloring TREES pt. 1
He is interested in knowing how many triplets (a,b,c) of vertices are there, such that, there is atleast one edge having red color on all the three paths i.e. from vertex a to b, vertex b to c and vertex c to a. Test your knowledge with our Tree Coloring practice problem.

Dive into the world of 4.