Definition Of Linear Graph
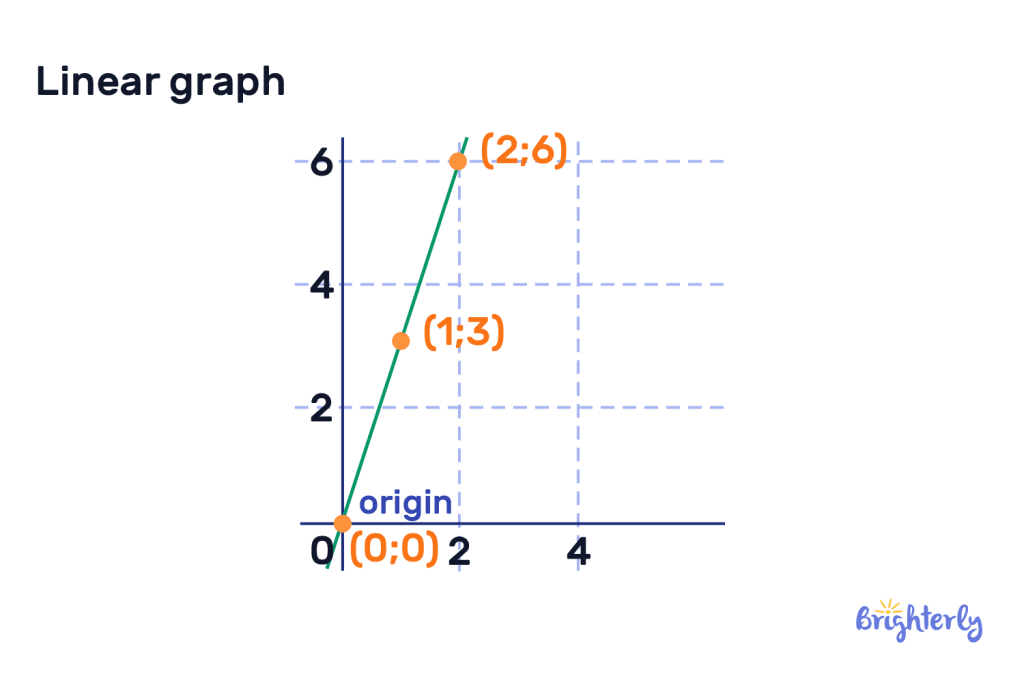
Linear Graph Definition A line graph with continuous or unbroken nature is called a linear graph. To draw the unbroken line we need to locate some points on the graph sheet. Let's make a graph with an x and y-coordinate.
Suppose you go to an auditorium and search for your reserved seat. You need to know two numbers, the row number, and the seat number. This is the basic method for fixing a.

How to draw linear graph? - with Examples - Teachoo - Making Linear Gr
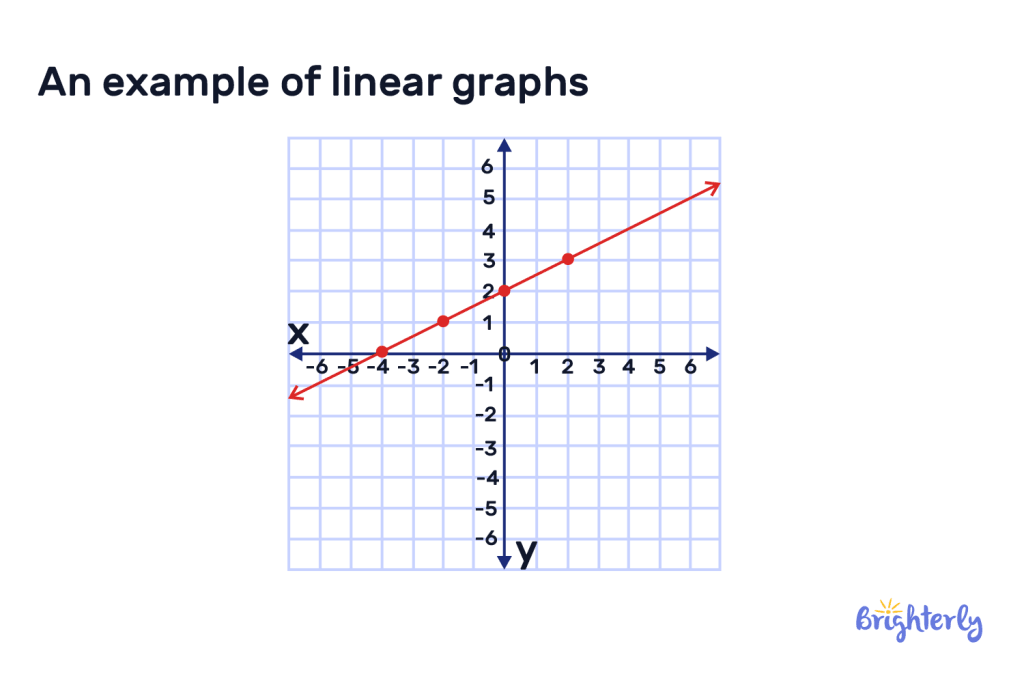
A linear graph is the graphical representation of a straight line. A graph when plotted gives a single straight line then it is known as a linear graph. A linear graph represents relationships between quantities using straight lines, defined by the equation y = mx + c, where m is the slope and c is the y-intercept.

All points on linear graphs are collinear, forming continuous straight lines with infinite solutions. Linear graphs are a key concept in math related to calculus and statistics. Learn about linear graphs with Brighterly.

Linear Graph - GCSE Maths - Steps, Examples & Worksheet
Linear Graph - Explanation and Examples A linear graph is a representation of a linear relationship in the Cartesian coordinate system. Essentially, a linear graph is a straight line plotted on the x y coordinate plane. Linear Graph Examples Let us understand the Linear graph definition with examples.
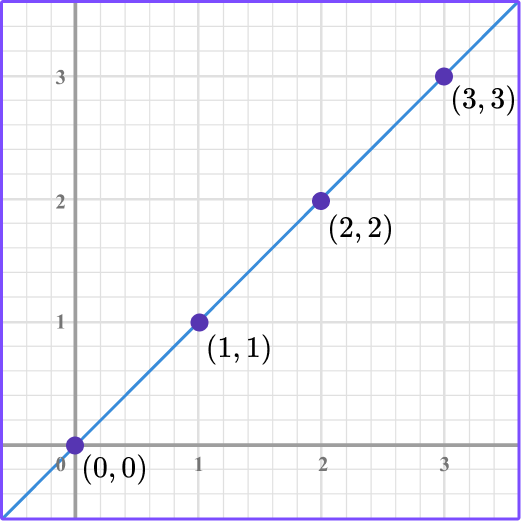
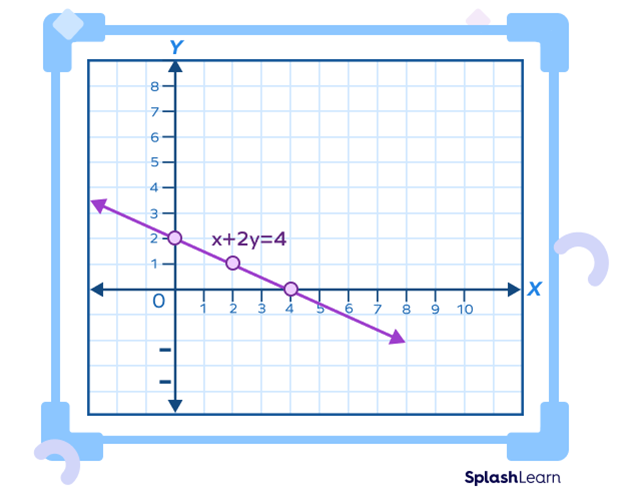
The equation y=2x+1 is a linear equation or forms a straight line on the graph. When the value of x increases, then ultimately the value of y also increases by twice of the value of x plus 1. Suppose, if we have to plot a graph of a linear equation y=2x+1.
Linear Graph - Definition, Examples | What is Linear Graph?
Free linear graph school math topic guide, including step-by-step examples, free practice questions, and more! Learn Linear Graph at Bytelearn. Know the definitions, see the examples, and practice problems of Linear Graph. Your one.

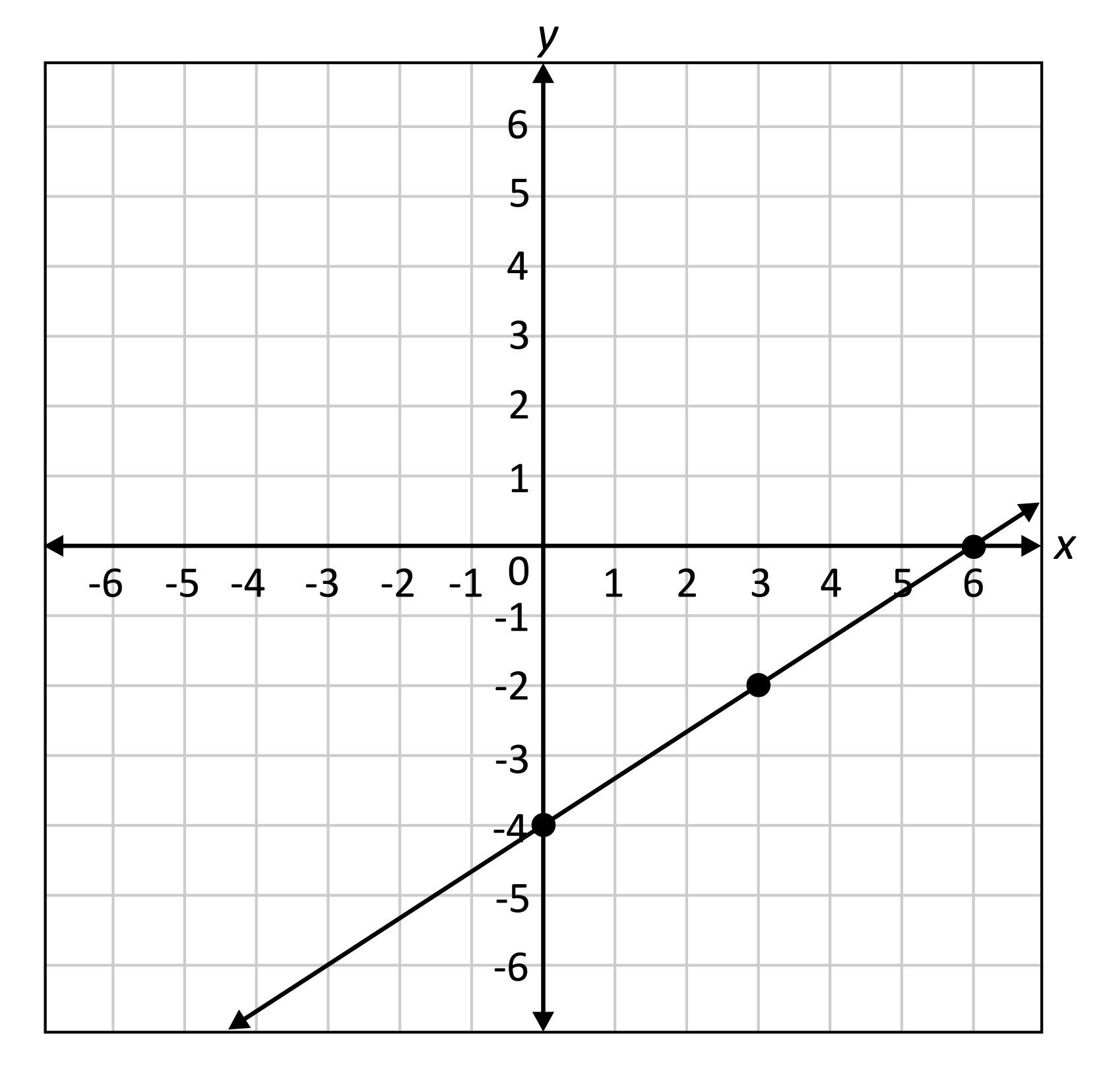
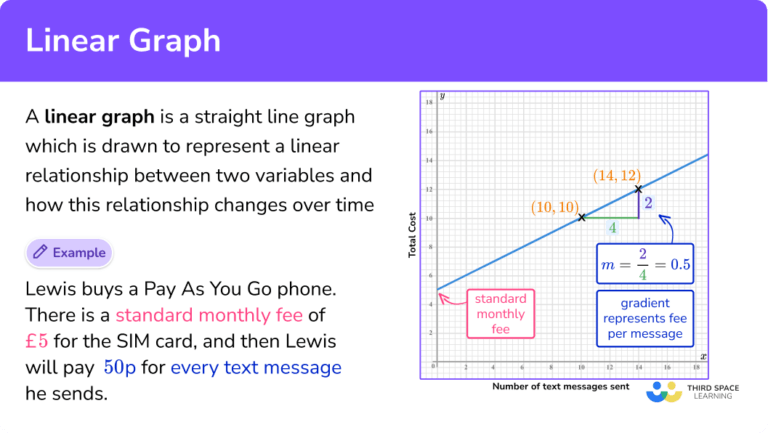
This section focuses on the key features and methods for working with linear graphs. It demonstrates how to sketch graphs from rules, derive rules from graphs, and calculate key features such as the gradient and \(x\)- and \(y\). A linear graph is defined as a straight line drawn on a coordinate plane to represent a linear equation, most often in the form y = m x + c.
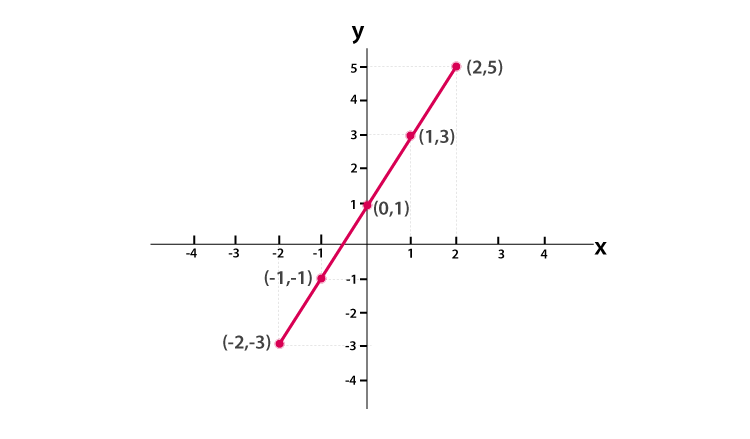
You'll find this concept applied in areas such as coordinate geometry, algebra, and data representation in practical scenarios.