3d Calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to functions of several variables: the differentiation and integration of functions involving multiple variables (multivariate), rather than just one. Explore math with our beautiful, free online graphing calculator. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more.

Here is a set of notes used by Paul Dawkins to teach his Calculus III course at Lamar University. Topics covered are Three Dimensional Space, Limits of functions of multiple variables, Partial Derivatives, Directional Derivatives, Identifying Relative and Absolute Extrema of functions of multiple variables, Lagrange Multipliers, Double (Cartesian and Polar coordinates) and Triple Integrals. Learn multivariable calculus-derivatives and integrals of multivariable functions, application problems, and more.
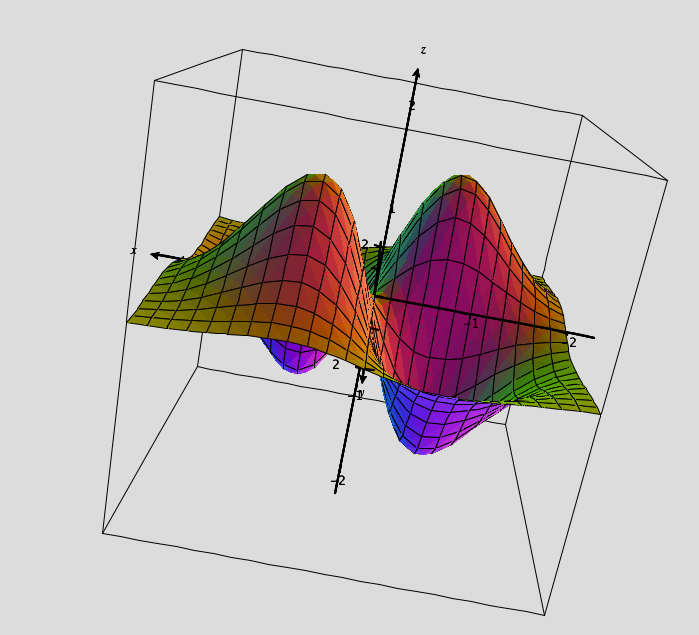
3d Calculus Graphs
Learn Multivariable Calculus (Calc 3) Online This course delves into the realm of differentiating functions of multiple variables and their practical applications. Exploring Multivariable Calculus! Welcome to Exploring Multivariable Calculus! This website is dedicated to helping you explore multivariable calculus, differential equations, and some three. Calculus 3 Visualizations Visualizations for Multivariable & Vector Calculus Left-click and drag to rotate pictures.
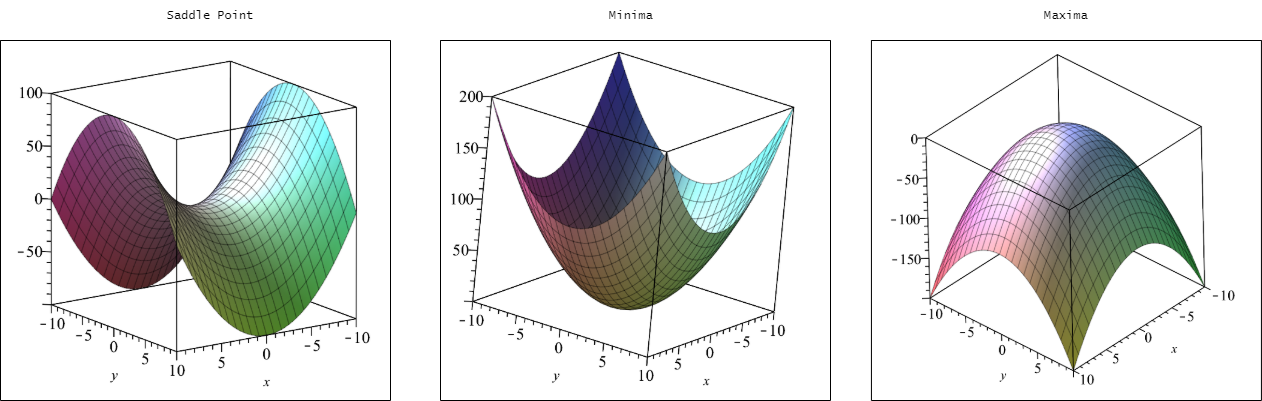
Right-click and drag to pan. Use the scroll wheel (or zoom gesture on touch screen) to zoom. Chapter 12 Section 12.1: 3D Coordinate Systems octants a point in 3D space a point in 3D space (user input) planes of the form variable.
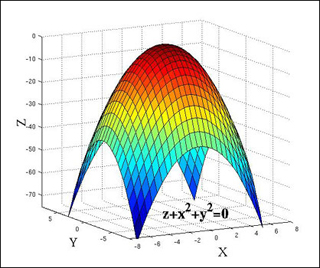
Calculus III - Functions of Several Variables
Calculus in 3Dis an accessible, well-written textbook for an honors course in multivariable calculus for mathematically strong fi rst. Manipulative Calculus is a project at Harvard University in which we are constructing 3D models and manipulatives to be used in active learning lessons in our calculus course sequence. Since Fall 2018, our models and lessons have been incorporated into Math 21a, Multivariable Calculus, at Harvard.
1. Introduction. In these notes we review the fundamentals of three-dimensional vector calculus.
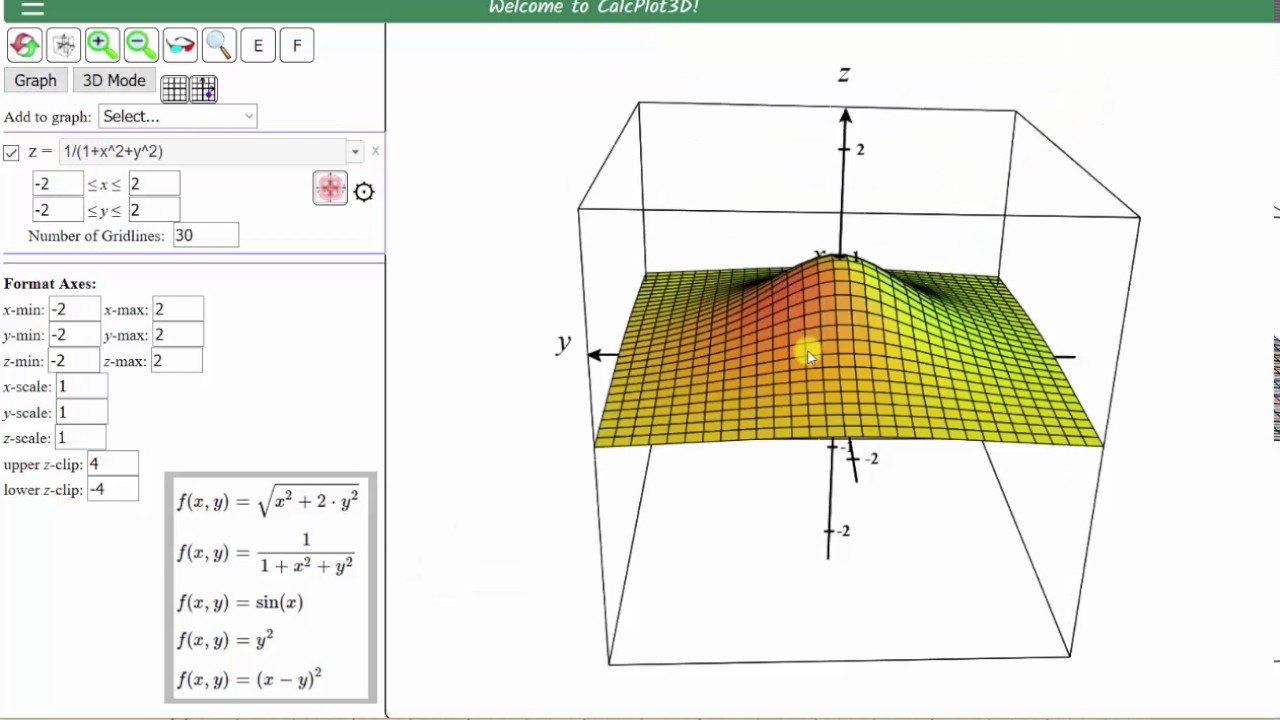
Using Interactive 3D Graphs to Increase Learning in Calculus Classes ...
We will be surveying calculus on curves, surfaces and solid bodies in three-dimensional space. The three methods of integration - line, surface and volume (triple) integrals - and the fundamental vector differential operators - gradient, curl and divergence.