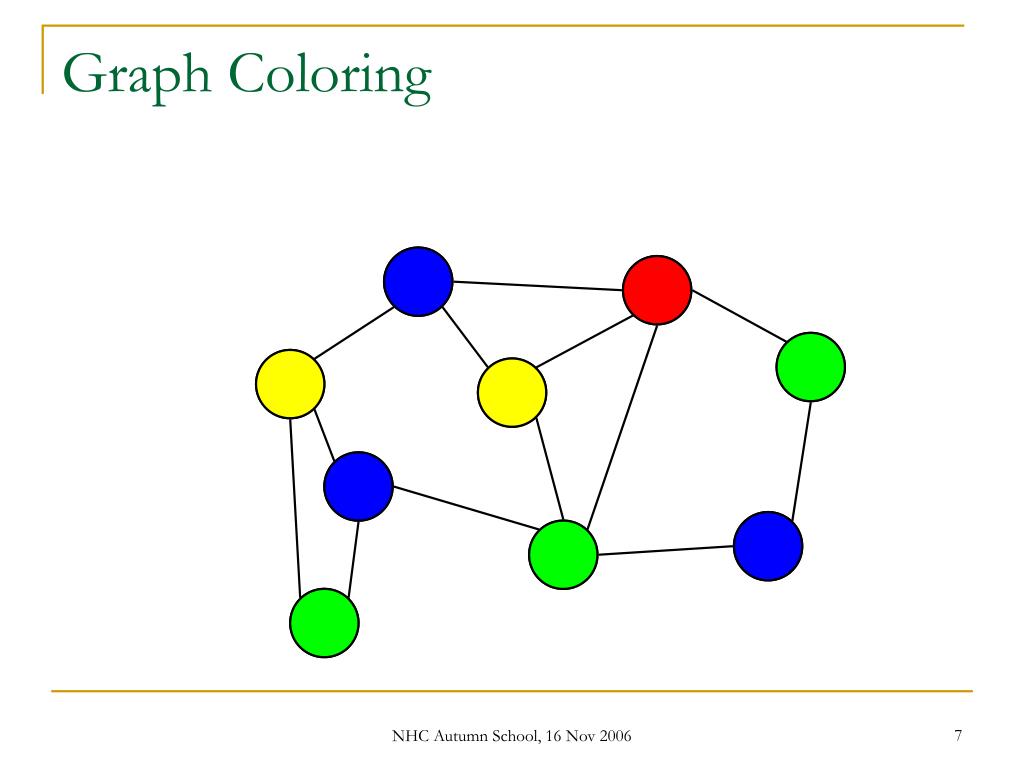
Approximate Graph Colouring And The Hollow Shadow

We show that approximate graph colouring is not solved by constantly many levels of the lift-and-project hierarchy for the combined basic linear programming and affine integer programming relaxation. The proof involves a construction of tensors whose fixed-dimensional projections are equal up to reflection and satisfy a sparsity condition, which may be of independent interest. c-colourable graph, where 3 ≤ c ≤ d.

There is a huge gap in our understanding of this problem. For an n-vertex graph and c = 3, the best known polynomial-time algorithm of Kawarabayashi, Thorup, and Yoneda [63] finds a d-colouring with d = ̃O(n0.19747), building on. ABSTRACT We show that approximate graph colouring is not solved by con-stantly many levels of the lift-and-project hierarchy for the com-bined basic linear programming and afine integer programming relaxation.

Figure 3 from Approximate Graph Colouring and the Crystal with a Hollow ... — www.semanticscholar.org

Figure 1 from Approximate Graph Colouring and the Crystal with a Hollow ...

The proof involves a construction of tensors whose fixed-dimensional projections are equal up to reflection and satisfy a sparsity condition, which may be of independent interest. Abstract. We show that approximate graph coloring is not solved by the lift.

Approximate Graph Colouring and the Hollow Shadow.Lorenzo Ciardo, Stanislav Zivny (University of Oxford). We show that approximate graph colouring is not solved by constantly many levels of the lift. Two new techniques to analyse the complexity of promise CSPs are introduced: one is based on topology and the other on adjunction, and these are applied together with the previously introduced algebraic approach to obtain new NP.

(PDF) Approximate Graph Colouring and the Hollow Shadow — www.researchgate.net

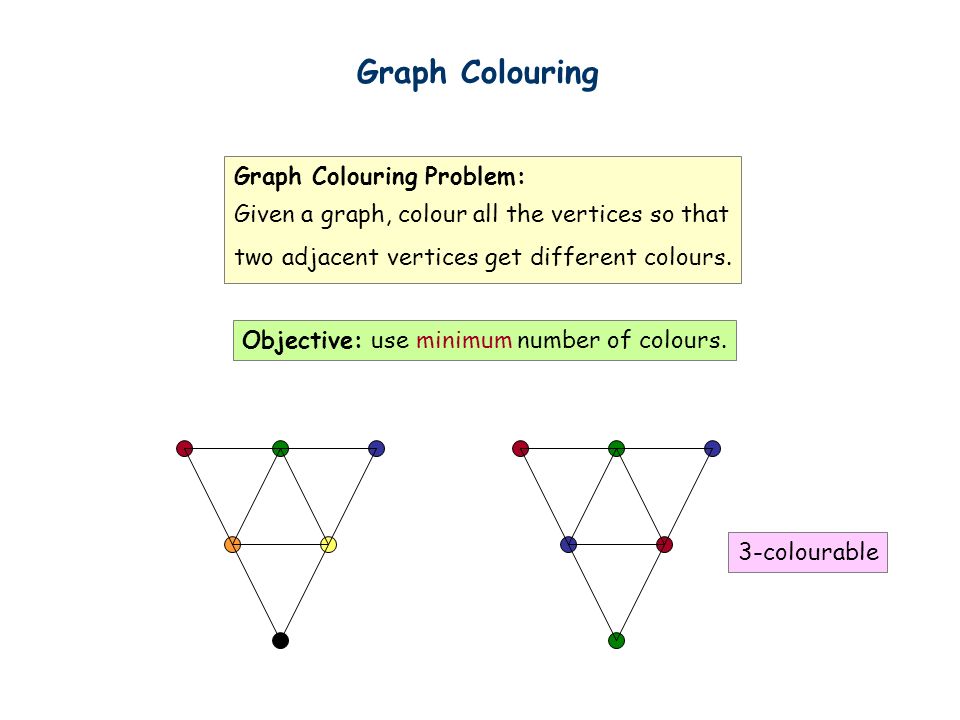
Graph Colouring Lecture 20: Nov 25. This Lecture Graph coloring is ...

1 Introduction The approximate graph colouring problem (AGC) consists in nding a d-colouring of a given c-colourable graph, where 3 c d. There is a huge gap in our understanding of this problem. For an n-vertex graph and c = 3, the currently best-known polynomial-time algorithm of Kawarabayashi and Thorup [58] nds a d-colouring with d = O(n0:19996), building on a long line of works started by.