4 Coloring Theorem
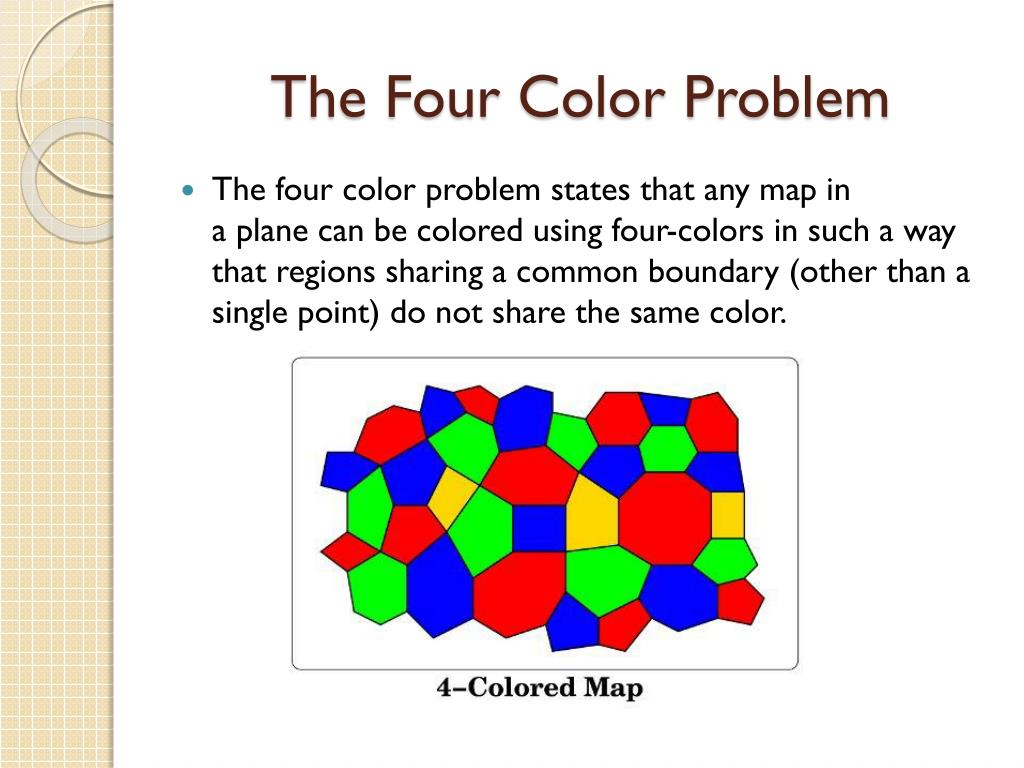
Four color theorem Example of a four-colored map A four-colored map of the states of the United States (ignoring lakes and oceans) In mathematics, the four color theorem, or the four color map theorem, states that no more than four colors are required to color the regions of any map so that no two adjacent regions have the same color. The four-color theorem states that any map in a plane can be colored using four-colors in such a way that regions sharing a common boundary (other than a single point) do not share the same color. This problem is sometimes also called Guthrie's problem after F.

Guthrie, who first conjectured the theorem in 1852. The conjecture was then communicated to de Morgan and thence into the general. Definition 1.4.

Discrete Structures for Computer Science - ppt download
A proper k-coloring of a graph is an assignment of one of k colors to each of its vertices such that no two adjacent vertices have the same color. Definition 1.5. A graph is k-colorable if there is a proper k-coloring of it.

Now, we are ready for a precise statement of the Four Color Theorem. Theorem 1.6 (Four Color Theorem). The Four Color Theorem and Kuratowski's Theorem are two fundamental results in discrete mathematics, specifically in the field of graph theory.

Four Color Theorem For Kids / This investigation will lead to one of ...
Both theorems address the properties of planar graphs but from different perspectives. In this article, we will understand about Four Color Theorem and Kuratowski's Theorem in Discrete Mathematics, their definition, examples, and semantic differences. The four color theorem states that any map--a division of the plane into any number of regions--can be colored using no more than four colors in such a way that no two adjacent regions share the same color.

The four color theorem is particularly notable for being the first major theorem proved by a computer. Interestingly, despite the problem being motivated by mapmaking, the theorem is not. THEOREM 1.
Four Color Theorem: What Is Four Color Map Theorem?
If T is a minimal counterexample to the Four Color Theorem, then no good configuration appears in T. THEOREM 2. For every internally 6-connected triangulation T, some good configuration appears in T.
From the above two theorems it follows that no minimal counterexample exists, and so the 4CT is true. The first proof needs a computer. 4.

Transforming the problem and finding new methods. Although Heawood found the major flaw in Kempe's proof method in 1890, he was unable to go on to prove the four colour theorem, but he made a significant breakthrough and proved conclusively that all maps could be coloured with five colours. The four-colour theorem (briefly, the 4CT) asserts that every loopless planar graph admits a vertex 4-colouring.
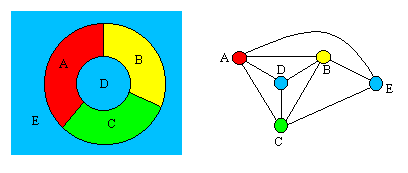
This was conjectured by Guthrie in 1852, and remained open until a proof was found by Appel and Haken [3 5] in 1976. Coloring (The Four Color Theorem) This activity is about coloring, but don't think it's just kid's stuff. This investigation will lead to one of the most famous theorems of mathematics and some very interesting results.

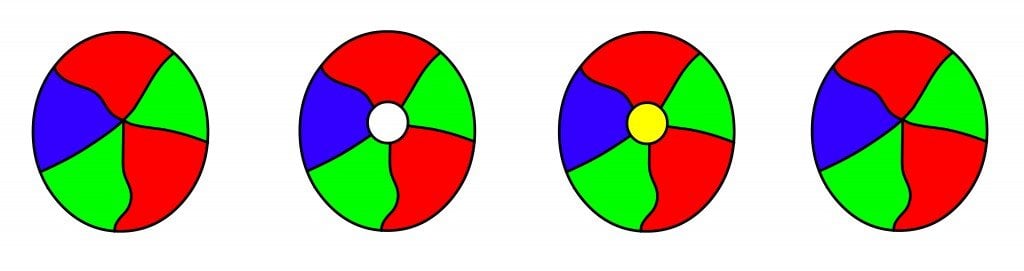
Have you ever colored in a pattern and wondered how many colors you need to use? There is only one rule. Four Color Theorem The four-color theorem states that any map in a plane can be colored using four-colors in such a way that regions sharing a common boundary (other than a single point) do not share the same color.