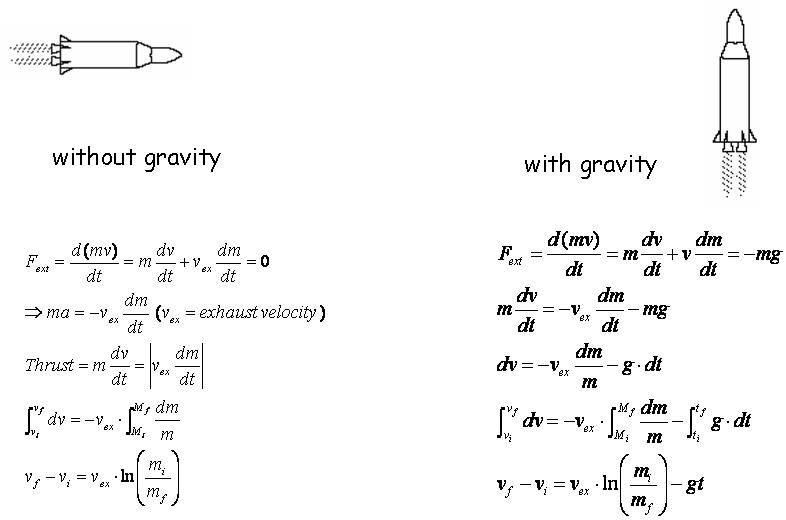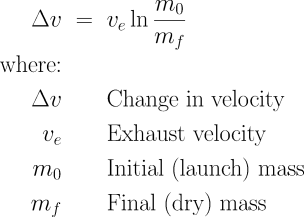Rocket Equation Example
Ideal Rocket Equation On this page: The forces on a rocket change dramatically during a typical flight. During powered flight, the propellants of the propulsion system are constantly being exhausted from the nozzle. As a result, the weight and mass of the rocket is constantly changing.

Because of the changing mass, we cannot use the standard form of Newton's second law of motion to determine. The classical rocket equation, or ideal rocket equation is a mathematical equation that describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high velocity and can thereby move due to the conservation of momentum. Learn how to use the ideal rocket equation, aka Tsiolkovsky rocket equation.

PPT - Rocket Trajectories PowerPoint Presentation, free download - ID ...
We explain its components in simple steps and show examples. 14. 2 The Rocket Equation We can now look at the role of specific impulse in setting the performance of a rocket.

A large fraction (typically 90%) of the mass of a rocket is propellant, thus it is important to consider the change in mass of the vehicle as it accelerates. This leads to exponential behavior-called the "rocket equation"-which puts tough limits on our ability to deliver large payloads to distant planets. In Part 1 of this article I'll develop the basic concepts of the rocket equation, and in part 2 apply the concepts to a worked example: the New Horizons mission to Pluto.

Equations For Ideal Rocket - ESRA - CSULB
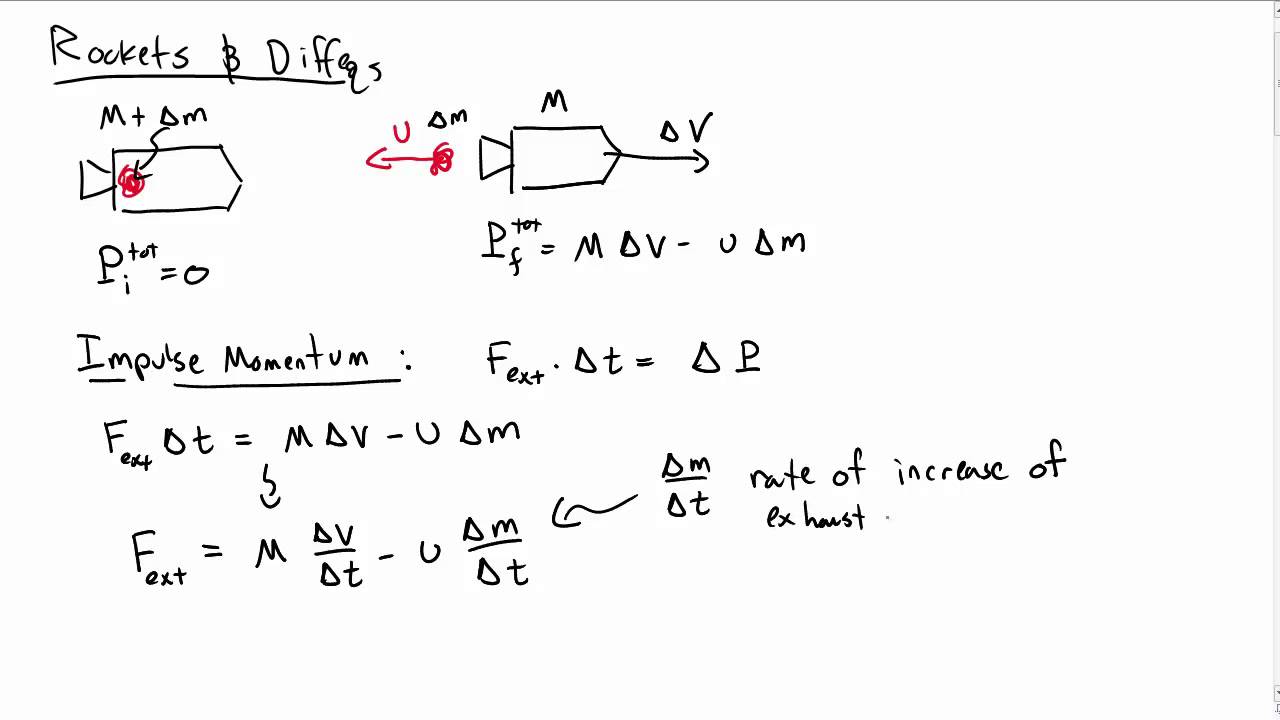
2.1 Tsiolkovsky's Rocket Equation Let us derive Tsiolkovsky's Rocket Equation (see, for example, [2]). We begin with the fundamental principle of conservation of momentum, taking into ac-count the rocket's decreasing mass over time as it expels fuel. As the rocket ejects fuel backward, it gains an equal amount of forward momentum, gener.

A rocket is an example of conservation of momentum where the mass of the system is not constant, since the rocket ejects fuel to provide thrust. The rocket equation gives us the change of velocity that the rocket obtains from burning a mass of fuel that decreases the total rocket mass. The rocket equation describes the motion of vehicles that follow the basic principle of a rocket: a device that can apply acceleration to itself using thrust by expelling part of its mass with high.

World of Engineering on Instagram: "The Tsiolkovsky rocket equation ...
k ROCKET EQUATIONS gravit accel g air density rho drag coef cd rocket body mr engine empty ee propellant mp rocket total mt engine init me propellant p% mass flow mü exhaust v vex diameter d c-s-area A drag factor k q qc2 qa p 9.8100 m/s2 1.2230 kg/m^3. Learn what the rocket equation is, how it limits space travel, and use our interactive calculator to test Starship and other rocket configurations. Ground hype with real math.