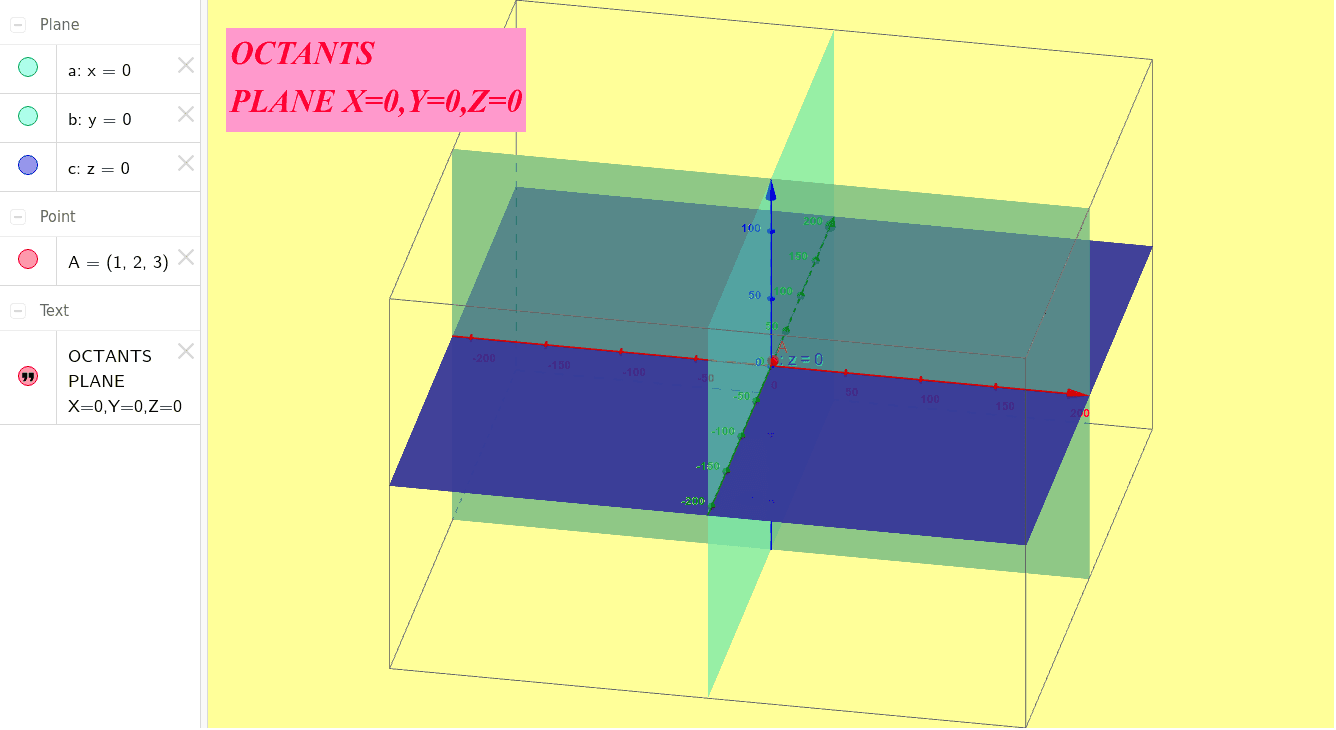
Octants 3d
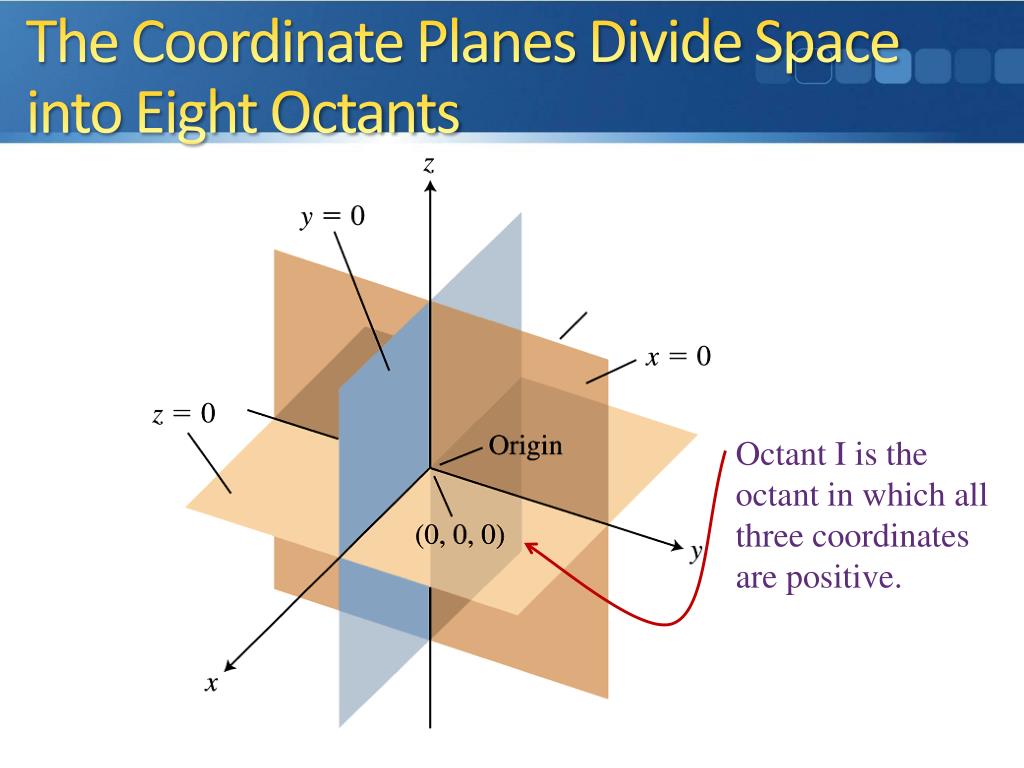
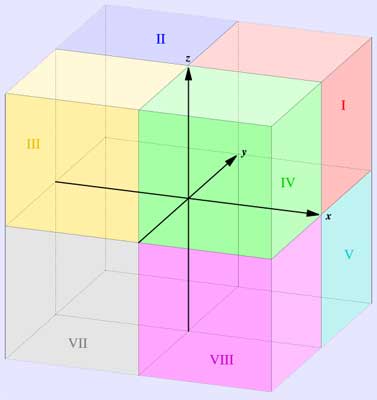
Three axial planes (x =0, y =0, z =0) divide space into eight octants. The eight (±,±,±) coordinates of the cube vertices are used to denote them. The horizontal plane shows the four quadrants between x - and y -axis.

(Vertex numbers are little-endian balanced ternary.) An octant in solid geometry is one of the eight divisions of a Euclidean three. Learn what an octant is in 3D geometry with clear definitions, sign conventions, visual representation, and solved examples. Understand how to identify points in different octants easily.

Octants – ToolNotes
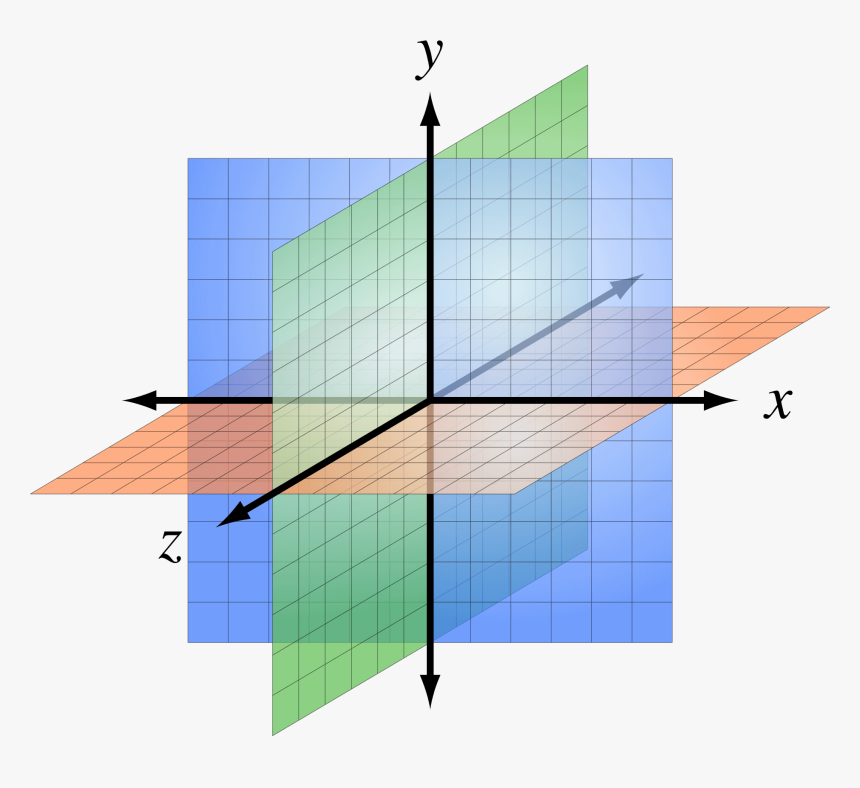
A three-dimensional coordinate system will have a total of eight octants that all intersect at the origin, O. If the 2D coordinate system has four quadrants, the 3D coordinate system has eight octants. The first octant will the three coordinates positive (similar to how the first quadrant has the positive x and y coordinates).
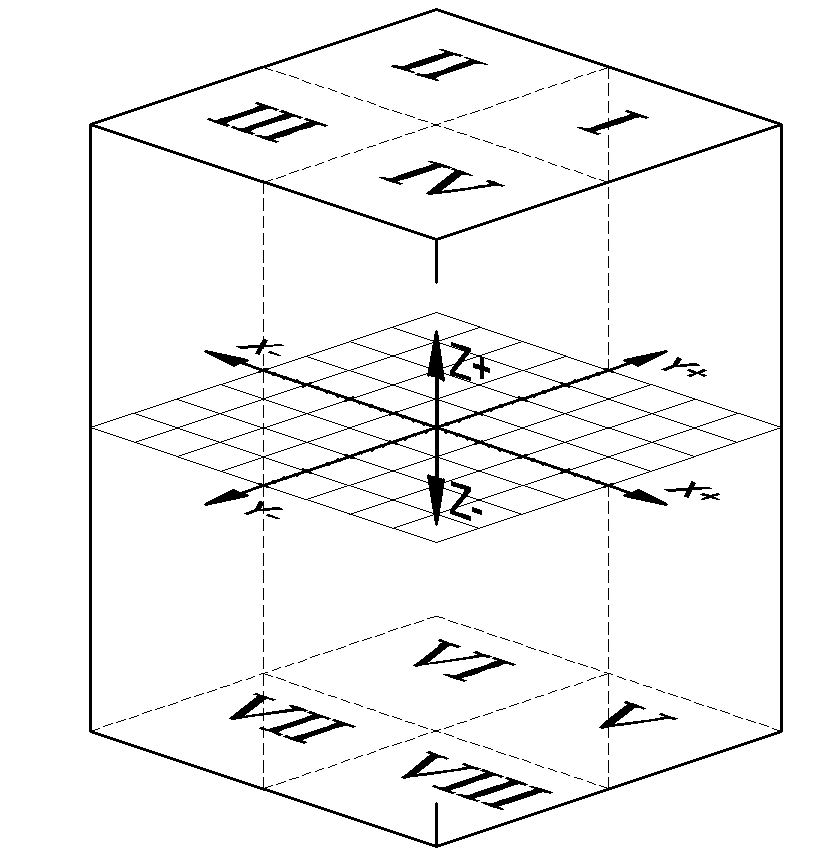
Figure 6. Points that lie in octants have three nonzero coordinates. Most work in three-dimensional space is a comfortable extension of the corresponding concepts in two dimensions.
Download Octants Coordinate System Three-Dimensional Spatial Geometry ...
In this section, we use our knowledge of circles to describe spheres, then we expand our understanding of vectors to three dimensions. Octants This 3D simulation shows all different octant of Euclidean three. One of the eight regions of space defined by the eight possible combinations of signs (+/-,+/-,+/-) for x, y, and z.

It happens to be the intersection of the two vertical planes. Any point in this space can now be identified with three coordinates with respect to these three axes. Rotate the planes below and see that that the whole space is divided into 8 distinct portions.
Octant in 3D Geometry: Definition, Sign Conventions, Representation ...
These are called octants. The first octant has points all whose coordinates will be. In three-dimensional space, three orthogonal planes intersect at right angles, creating a coordinate system defined by three orthogonal axes (x, y, and z).

These planes divide space into eight octants, each with a unique sign combination for the axis coordinates. This framework allows for precise location and measurement within the three. There is currently no standardized numbering system for the octants in three-dimensional space, although most people identify the region with +x, +y, and +z as the first octant.
The method used to identify the octants is to indicate verbally the portion of space they occupy. Octants are the eight distinct regions created by dividing three-dimensional space using the coordinate axes. Each octant represents a unique combination of positive and negative values for the x, y, and z coordinates, allowing for a structured way to describe the position of points in 3D space.

Understanding octants is crucial for visualizing geometric concepts and for navigating through.