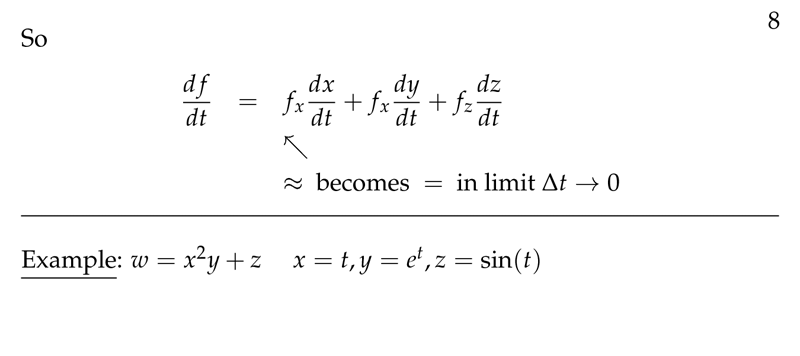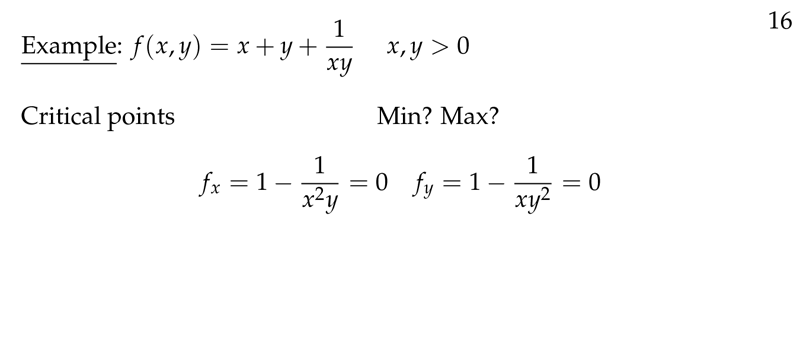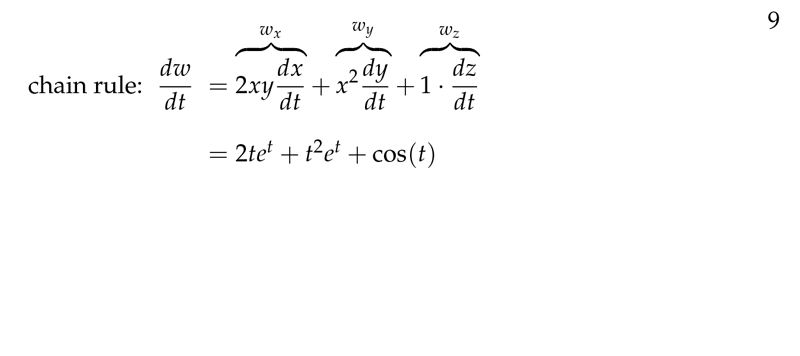Multivariable Calculus Examples
We extend our study of multivariable functions to functions of three variables. (One can make a function of as many variables as one likes; we limit our study to three variables.). In multivariable calculus, the candidates for maxima and minima are points at which the gradient equals the zero vector or does not exist.

This is a sensible generalization since the gradient of a single. Learn multivariable calculus-derivatives and integrals of multivariable functions, application problems, and more. Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to functions of several variables: the differentiation and integration of functions involving multiple variables (multivariate), rather than just one.

Session 48: Examples of Double Integration 5 | Multivariable Calculus ...
These partial derivatives, as regular single variable calculus derivatives in a single direction, satisfy all of the rules that one developed in Calculus I. Now, for a point (a; b) in the domain where these two quantities exist, the two tangent lines sitting in R3, cross at the point (a; b; f(a; b)) ∈ R3 and are perpendicular (form a right. Examples: Given some functions of 2 variables: find the domain, evaluate the function at a point.

(rational function, exponential and logarithm function) Example 7.1.5 p 560 (both part a and b): The Cobb-Douglas production functions Q K, L = AK L where Q is the output at a factory, K is the amount of capital investment, L is the size of the. MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity.

Intro to Multivariable calculus - 5 Introduction to multivariable ...
In this direction, multivariable calculus plays an important role. It has various applications starting from economics to science. In this tutorial, we will learn about multivariable calculus and its various operations (such as limits, continuity, partial derivatives, and integration) with solved examples.

Unlock multivariable calculus basics, examples, and exam tips. Boost your grades-learn with Vedantu's expert guidance! For example, here is the graph of \ (z = 2 {x^2} + 2 {y^2} - 4\). This is an elliptic paraboloid and is an example of a quadric surface.
Session 33: Examples 1 | Multivariable Calculus | Mathematics | MIT ...
We saw several of these in the previous section. We will be seeing quadric surfaces fairly regularly later on in Calculus III.