Rainbow Vertex Coloring
Rainbow coloring of a wheel graph, with three colors. Every two non-adjacent vertices can be connected by a rainbow path, either directly through the center vertex (bottom left) or by detouring around one triangle to avoid a repeated edge color (bottom right). RAINBOW INDUCED SUBGRAPHS IN PROPER VERTEX COLORINGS ANDRZEJ KISIELEWICZ AND MAREK SZYKULA that every proper vertex coloring of G contains a rainbow induced subgraph isomorphic to H.

We give upper and lower bounds for ρ(H), compute the exact value for some classes of graphs, and. A proper vertex coloring of a connected graph G that results in a vertex rainbow-connected graph is a vertex rainbow coloring of G. The minimum number of colors needed in a vertex rainbow coloring of G is the vertex rainbow connection number vrc (G) of G.

(a) Rainbow vertex coloring of í µí°¾ 6 , and (b) Locating rainbow ...
Thus if G is a connected graph of order n ≥ 2, then 2 ≤ vrc (G) ≤ n. In the Rainbow Vertex Coloring (RVC) problem we want to decide whether the vertices of a given graph can be colored with at most k colors so that the graph becomes rainbow vertex-connected. This problem is known to be NP-complete even in very restricted scenarios, and very few efficient algorithms are known for it.

First get a rainbow coloring of the connected dominating set. Then color the remaining edges in such a way that for each vertex x outside there are two disjoint rainbow colored paths (rainbow colored using different set of colors). Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory.

Rainbow -vertex colouring of subdivision graph of Friendship graph í µí ...
We undertake a study on rainbow vertex. Abstract - Rainbow vertex coloring introduced a decade ago followed by Rainbow dominator Coloring in recent years has been at tracting the researchers in graph theory. We undertake a study on rainbow vertex coloring and in particular rainbow dominator coloring for specific connected graphs namely Bull graph, Star graph, Complete graph, Helm graph and sunlet graph, Jelly fish, Jewel graph.

In this paper the rainbow coloring of double triangular snake DTn was defined and the rainbow connection numbers rc(G) and rvc(G) have been computed. Keywords -Rainbow connection number, rainbow vertex connection number, double triangular snake. The smallest number needed to color G so that it is rainbow vertex-disconnected is known as the rainbow vertex-disconnection number of G, or r v d (G).

(PDF) Algorithms for the rainbow vertex coloring problem on graph classes
The RVD. The Rainbow Vertex Coloring (RVC) problem takes as input a graph G and an integer k and asks whether G has a coloring with k colors under which it is rainbow vertex-connected. The rainbow vertex connection number of a graph G is the smallest number of colors needed in one such coloring and is denoted rvc(G).





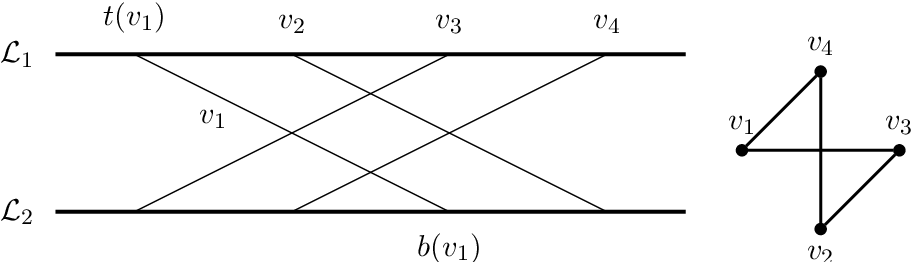
![A rainbow vertex 2 n -coloring on Pc n , for n ∈ [2 , 7] | Download ... A rainbow vertex 2 n -coloring on Pc n , for n ∈ [2 , 7] | Download ...](https://www.researchgate.net/publication/289994339/figure/fig1/AS:324971160195089@1454490570858/A-rainbow-vertex-2-n-coloring-on-Pc-n-for-n-2-7.png)