What Is Free Vector In Physics
The conversation emphasizes that in non-Cartesian coordinates, a vector's representation changes based on its location, making it non-free. Overall, the distinction between free and non. 8 When considering basic Newtonian mechanics, we can treat vector as free and move their point of application at will.
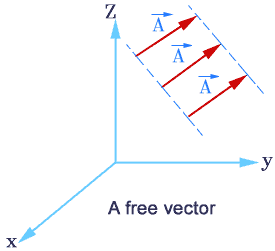
This is consistent with the affine nature of Euclidean space. However, when calculating torque on a body, we must treat forces as bound to their point of application. What is the mathematical reason for this? Unit, Free, Forced & Fixed VectorUNIT VECTOR: A unit vector is defined as a vector in any specified direction whose magnitude is unity i.e.
Symbols of physics Royalty Free Vector Image - VectorStock
1. A unit vector only specifies the direction of a given vector. " A free vector: is one whose action is not confined to or associated with a unique line in space.

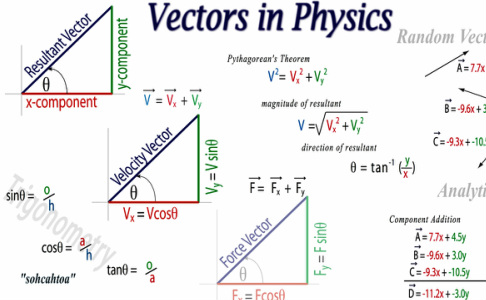
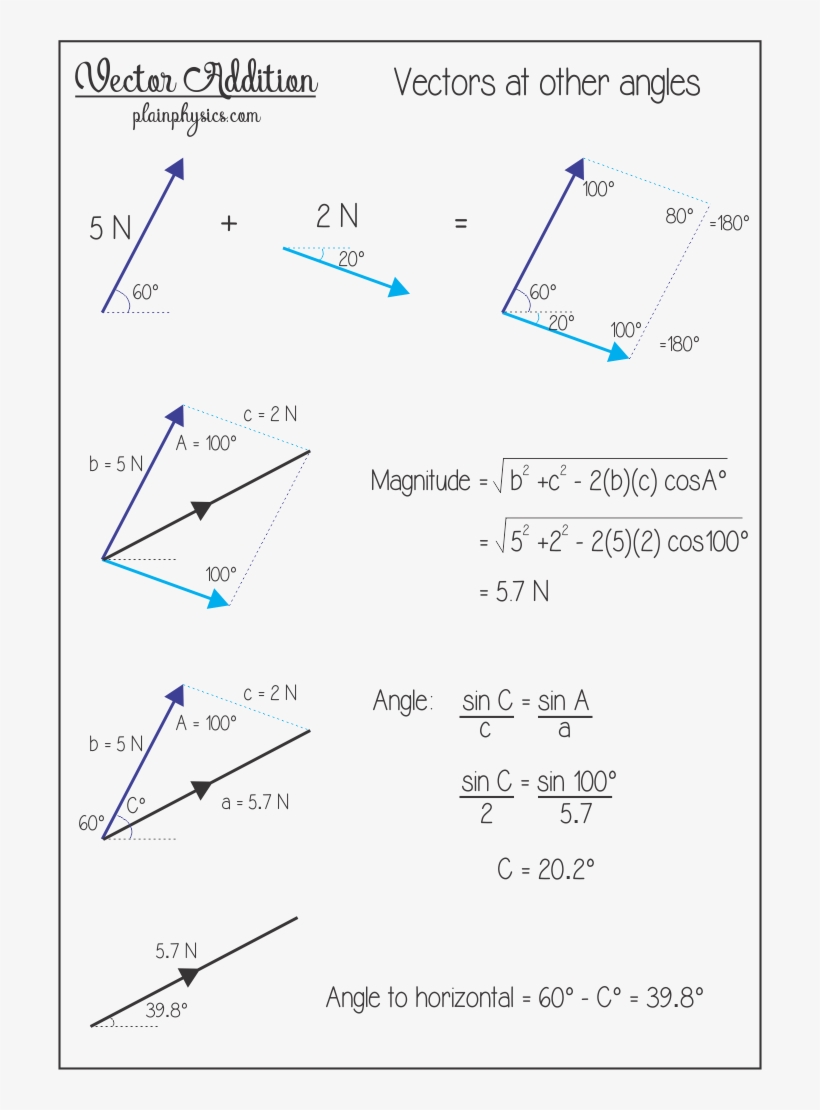
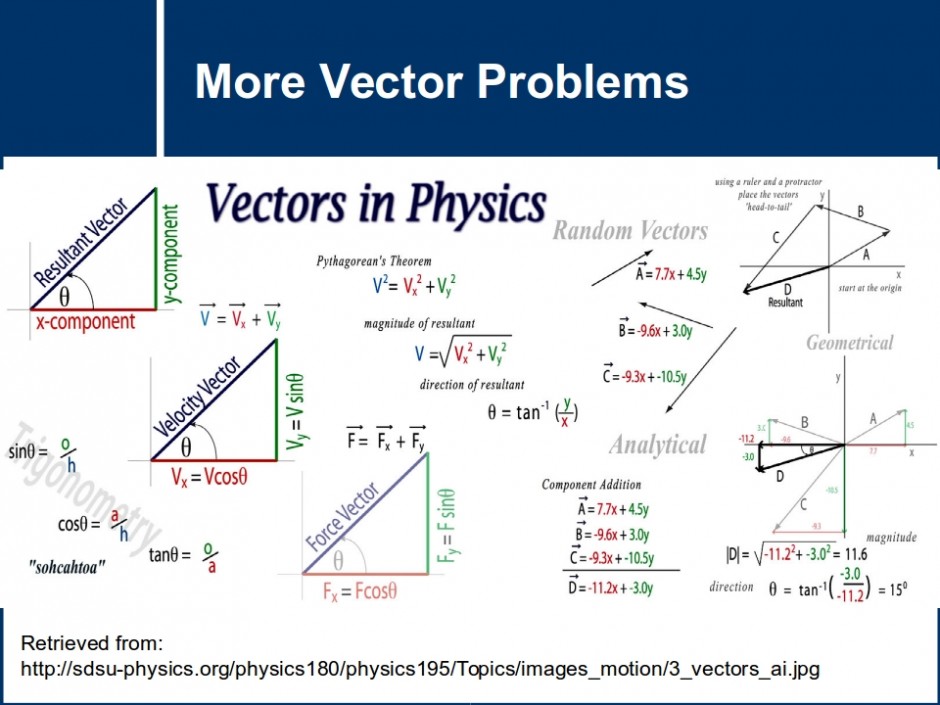
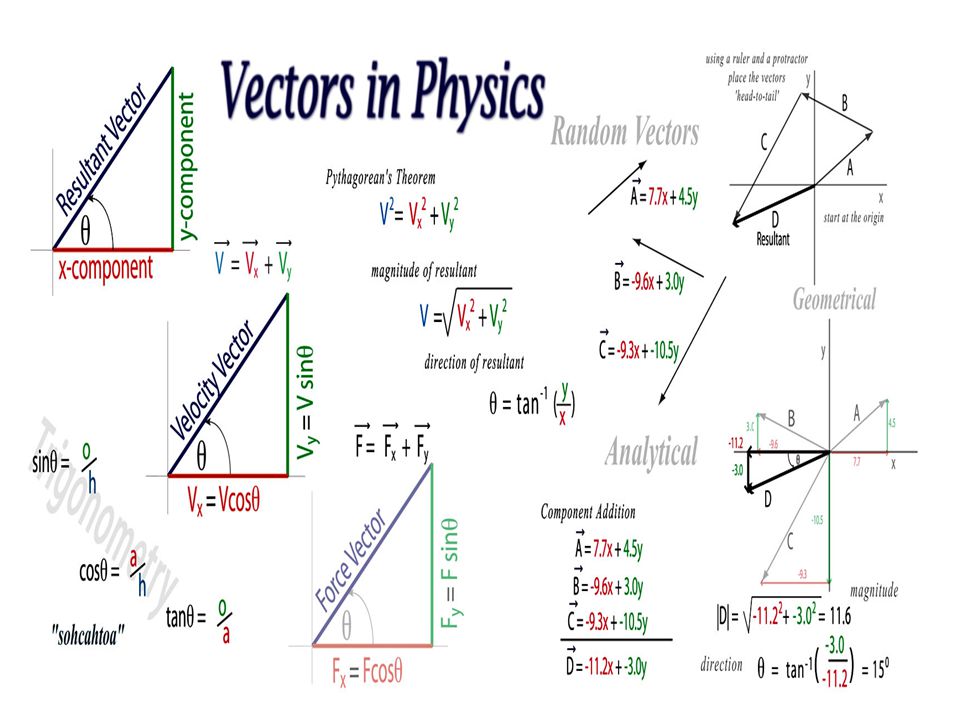
For example if a body is in translational motion, velocity of any point in the body may. Decomposing a vector into horizontal and vertical components is a very useful technique in understanding physics problems. Whenever you see motion at an angle, you should think of it as moving horizontally and vertically at the same time.
What is a Vector? (Physics) - YouTube
Simplifying vectors in this way can speed calculations and help to keep track of the motion of objects. A vector whose point of application is not fixed but magnitude and direction is fixed. This video is about: Free vector.

Subscribe to our YouTube channel to watch more Physics lectures. Practice. Microwave-Free Vector Magnetometry with Nitrogen-Vacancy Centers along a Single Axis in Diamond Sensing vector magnetic fields is important to many applications in fundamental physics, bioimaging, and materials science.

What Is A Vector Quantity In Physics Examples at Dwight Dees blog
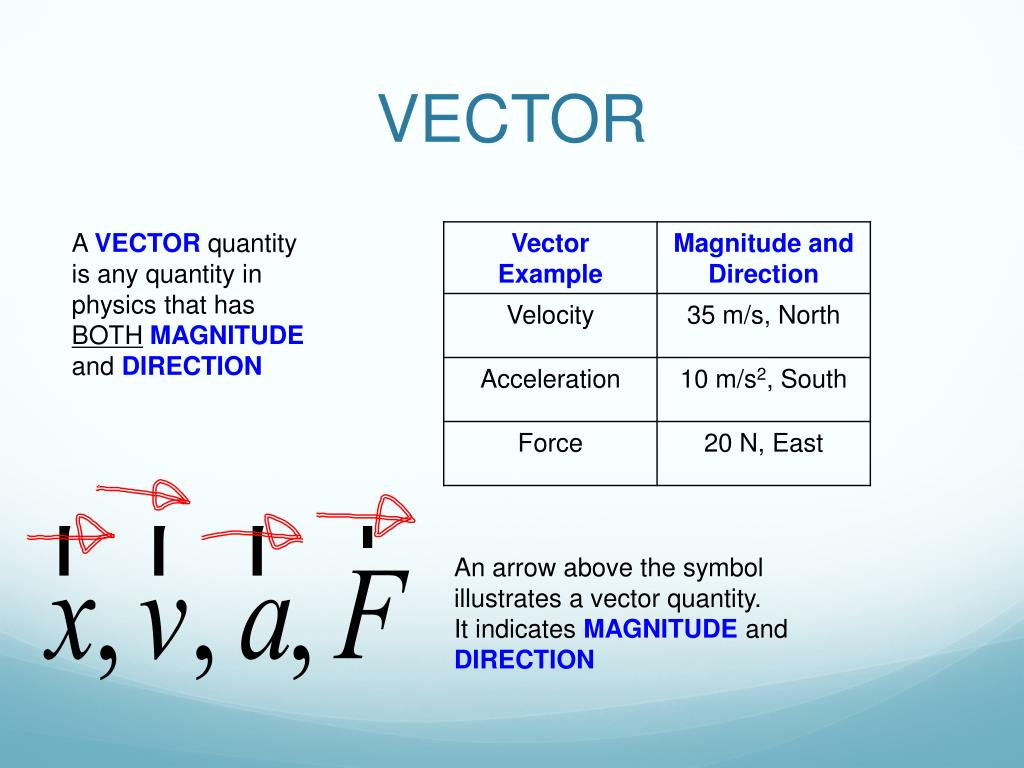
Vectors and Units Introduction Vectors and units are foundational concepts that form the backbone of quantitative descriptions in mathematics, physics, engineering, and computer science. They provide a structured and consistent way to represent physical quantities such as force, velocity, displacement, and acceleration, each of which requires both magnitude and direction to be fully described. The Use of Vectors in Physics From the last section we have three important ideas about vectors: vectors can exist at any point \ (P\) in space, vectors have direction and magnitude, and any two vectors that have the same direction and magnitude are equal no matter where in space they are located.

When we apply vectors to physical quantities it's nice to keep in the back of our minds all.