A Kirby Color For Khovanov Homology
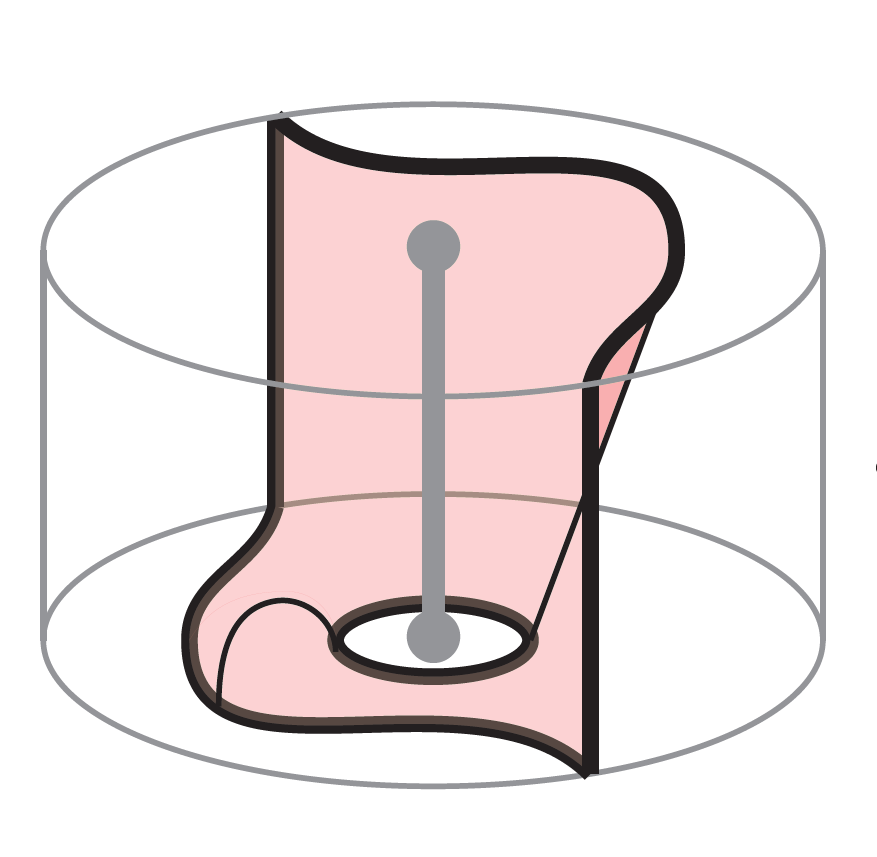
We construct a Kirby color in the setting of Khovanov homology: an ind-object of the annular Bar-Natan category that is equipped with a natural handle slide isomorphism. Using functoriality and cabling properties of Khovanov homology, we define a Kirby-colored Khovanov homology that is invariant under the handle slide Kirby move, up to isomorphism. Via the Manolescu.

We construct a Kirby color in the setting of Khovanov homology: an ind-object of the annular Bar-Natan category that is equipped with a natural handle slide isomorphism. Using functoriality and cabling properties of Khovanov homology, we define a Kirby-colored Khovanov homology that is invariant under the handle slide Kirby move, up to isomorphism. Abstract: In this talk I will discuss how to construct an object of the annular Bar-Natan category (rather, a completion thereof) which satisfies handle.
All selectable colors in Kirby Air Ride netplay : r/Kirby
Via functoriality/cabling properties of Khovanov homology, we define a Kirby-colored Khovanov homology that is invariant under the handle slide Kirby move, up to isomorphism. In this talk I will discuss how to construct an object of the annular Bar-Natan category (rather, a completion thereof) which satisfies handle-slide invariance. This work is joint with Dave Rose and Paul Wedrich, and is intended to yield a simplification (and ultimately a chain-level refinement of) the Manolescu.

In this context, the pair (K,V) is called a colored knot, and its Khovanov invariant is called colored Khovanov homology. In my talk I will discuss recent joint work with David Rose and Paul Wedrich, in which we construct an object in ABN (more accurately, an ind-object therein), called a Kirby color, whose associated colored Khovanov invariant. Abstract.

Kirby Color Chart! by jewelsio on DeviantArt
We construct a Kirby color in the setting of Khovanov homology: an ind-object of the annular Bar-Natan category that is equipped with a natural handle slide isomorphism. Using functo-riality and cabling properties of Khovanov homology, we de ne a Kirby-colored Khovanov homology that is invariant under the handle slide Kirby move, up to isomorphism. Via the Manolescu{Neithalath.

preprint, 58 pp. A Kirby color for Khovanov homology (joint with Matthew Hogancamp and Paul Wedrich), 47 pp. To appear in Journal of the European Mathematical Society (JEMS).

A Kirby color for Khovanov homology | EMS Press
A note on the Sundaram-Stanley bijection (or, Viennot for up-down tableaux) (joint with Elijah Bodish, Ben Elias, and Logan Tatham), preprint, 14 pp. A Kirby color for Khovanov homology In the context of quantum link invariants, a Kirby color is a linear combination of cabling patterns with the property that the resulting colored link polynomial is invariant under the second (handle slide) Kirby move.







