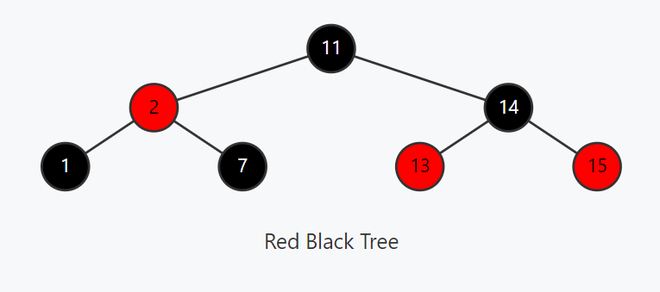
Red Black Tree Coloring
The duality of color in red-black trees is a key part to all four of its rules, and an important part of keeping the tree balanced. But why were red-black trees created with colors in mind? Example of a red-black tree In computer science, a red-black tree is a self-balancing binary search tree data structure noted for fast storage and retrieval of ordered information. The nodes in a red-black tree hold an extra "color" bit, often drawn as red and black, which help ensure that the tree is always approximately balanced.

[1]. What is a Red-Black Tree? A Red-Black Tree is a self-balancing binary search tree where each node has an additional attribute: a color, which can be either red or black. The prima.
redblacktrees
I've been teaching algorithms and data structures for a couple of years now and my honest advice about red/black trees is the following: Know where the rotation rules and color flips come from, but don't memorize them. It's extremely uncommon to actually need to trace through red/black tree rotations by hand or to have to code them up. In those cases, I'd recommend doing what most people do.

Lookup A red black tree is a BST. Lookup in an RBT is just lookup in a BST. The colors don't matter.

All About Red-Black Trees
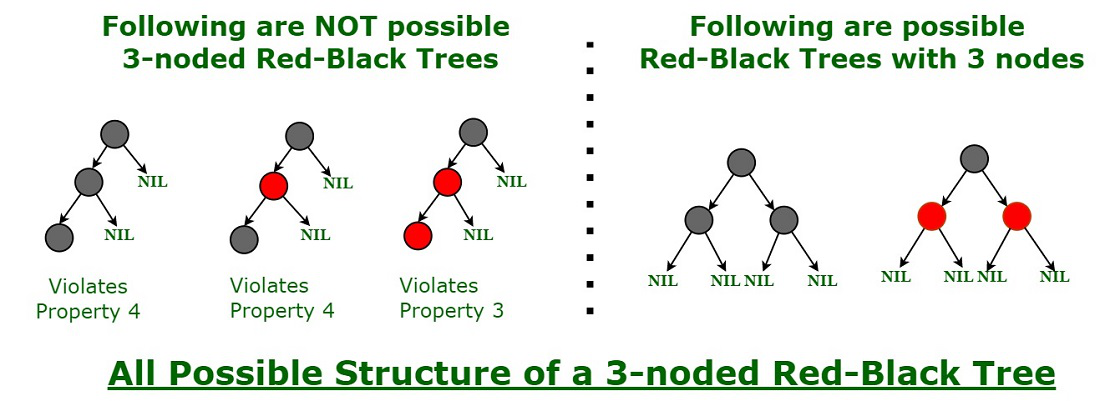
Insertion The algorithm has three steps: Insert as you would into a BST, coloring the node red. If the parent of the node you just inserted was red, you have a double. Red-Black Trees For each of the following examples, if the nodes can be colored red or black to make a legitimate red-black tree, then give such a coloring.
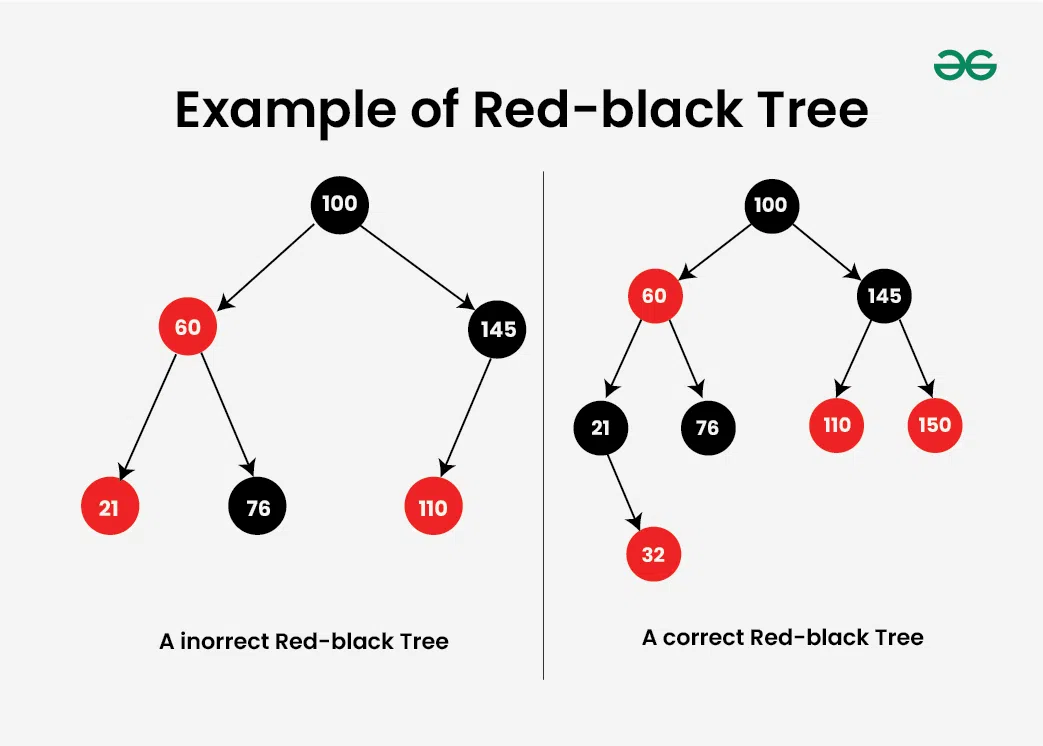
If not, then say that they cannot. Red-Black trees are self-balancing binary search trees that use node coloring to maintain balance. They offer efficient searching, insertion, and deletion operations with a time complexity of O (log n), making them a crucial topic in the study of balanced trees.
CSC 421: Algorithm Design Analysis - ppt download
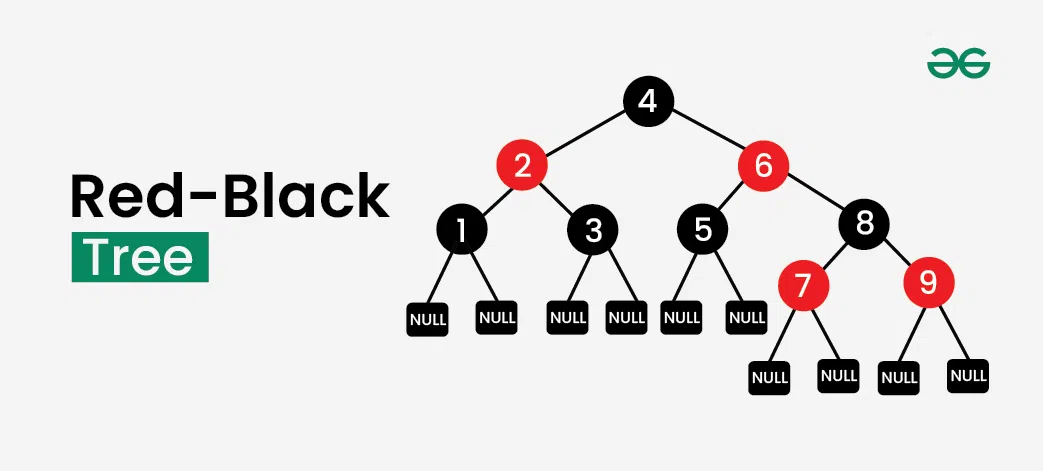
These trees strike a balance between the strict AVL tree structure and the more relaxed B. Red-Black Tree Height Bound Red-black tree rules constrain the adjacency of node coloring, ensuring that no root-to-leaf path is more than twice as long as any other path, which limits how unbalanced a red. Red-black trees are binary search trees that store one additional piece of information in each node (the node's color) and satisfy three properties.
+such+that..jpg)
These properties deal with the way nodes can be colored (the root property and the red property) and the number of black nodes along paths from the root node to a null child pointer (the black. On this page, you will find 38 unique tree coloring pages that are all free to download and print! While trees are something we see on a daily basis, they are often overlooked and under-appreciated in how important they are to our survival. If you would like to show your appreciation for trees, don't "leave," as this is the post for you!