Applications Of Graph Coloring In Computer Science
Graph coloring is one of the most important concepts in graph theory and is used in many real time applications in computer science. The main aim of this paper is to present the importance of. Graphs have a very important application in modeling communications networks.

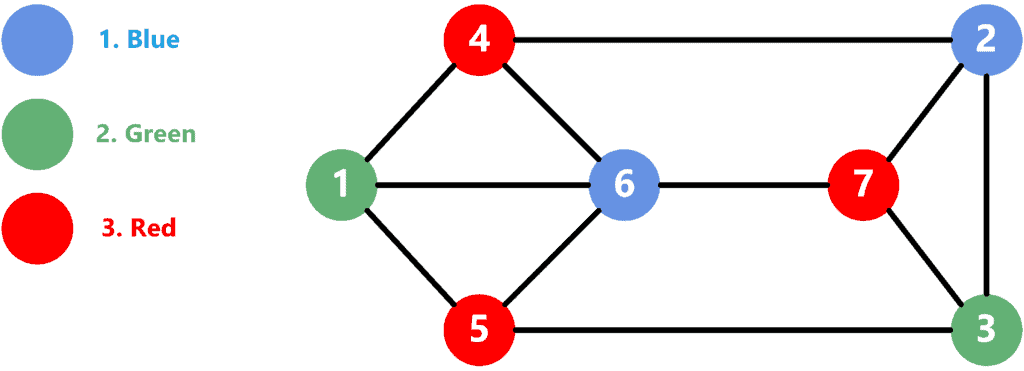
Graph coloring is an effective technique to solve many practical as well as theoretical challenges. In this paper, we have presented applications of graph theory especially graph coloring in team-building problems, scheduling problems, and network analysis. The optimization problem is stated as, "Given M colors and graph G, find the minimum number of colors required for graph coloring." Algorithm of Graph Coloring using Backtracking: Assign colors one by one to different vertices, starting from vertex 0.

Graph coloring using backtracking | PPTX
Before assigning a color, check if the adjacent vertices have the same color or not. Graph coloring is a fundamental concept in graph theory, a branch of mathematics that studies the properties and applications of graphs. In computer science, graph coloring has numerous applications in various fields, including computer networks, scheduling, and resource allocation.
Graph theory is rapidly becoming into the mainstream of mathematics mainly because of its applications in various fields which include physics, biology, chemistry, electrical engineering, computer science, operation research etc. In computer science the ideas of graph theory are highly utilized (Daniel M, 2004) [1]. Graph theory, one of the most important topic of computer science carries a great significance in algorithms and data structure.

Graph Coloring | PPTX | Geography | Science
It is. Abstract "Graph coloring is one of the most important concepts in graph theory and is used in many real time applications in computer science. The main aim of this paper is to present the importance of graph coloring ideas in various areas of compute applications for researches that they can use graph coloring concepts for the research.

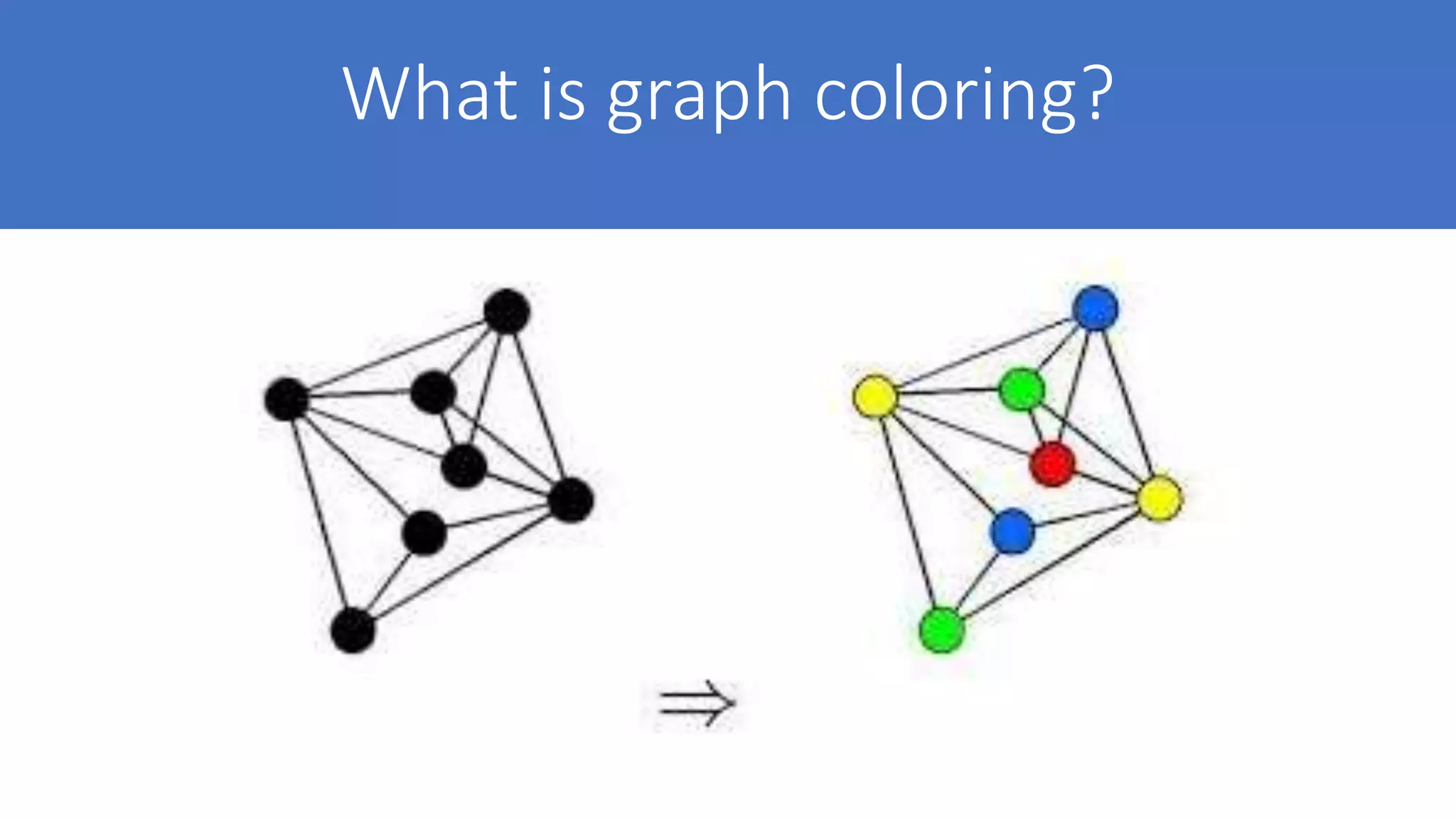
A graph coloring is an assignment of labels, called colors, to the vertices of a graph such that no two adjacent vertices share the same color.Applications for solved problems have been found in areas such as computer science, information theory, and complexity theory. Graph coloring is mainly used in research fields of computer science like networking, data mining, image processing etc. Modeling of network topologies, data base design, schedul-ing, travelling salesman problem, guarding art gallery are some of the applications that use graph coloring concept.

(PDF) Applications of Graph Coloring and Labeling in Computer Science
Shamim Ahmed Abstract.